Finshing Jim's Model and starting Pablo's

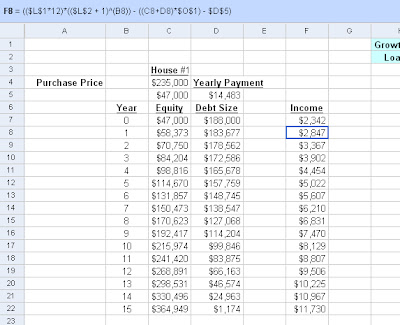
Last post we talked about figuring out how Jim's one house was going to grow in value over 20 years. We got up to year 15, where he only owed just over $1,000 on his house, which was now worth $365,000 and generated more than $2,000 a month in rental revenue.

Today let's talk about what's happening in year 16, when Jim starts saving for rental home #2, and let's see what happens from then until year 20, when our model will stop.

Going into year 16 we make a couple of manual modifications to our model. We have to modify the equity that we're taking to no longer account for our debt (because there no longer will be any), and we have to modify our income (which stands for annual income after expenses). Instead of subtracting the annual mortgage payments ($14,483) we only need to subtract $1,174, which is the amount left in our mortgage.

At the end of year 16 the house is now earning $25,950 a year after property taxes and insurance. In addition Jim now has $24,961 in his bank account. But since houses are now worth $377,000 in his area and we want to put 10% down, we're going to wait another year before buying.

In Year 17 the picture changes. We now have $50,000 in the bank, and with houses costing $388,00 Jim is going to go ahead and buy one. We then create a second set of columns for the second house and expand upon them.


The result is that at the end of 20 years Jim has a annual income (after property taxes, mortgage payments and insurance) of nearly $35,000. At the rate things are going, he will pay off the second house in less than 5 more years (year 25) at which point he'll have an annual income of more than $70,000 (after property taxes and insurance). If Jim is 30 years old, then he can look forward to having nearly a full salary each year just from his business, not even beginning to count the savings he hopefully has put aside for retirement through his day job.

Now this result needs some very important explanations. One critical assumption here is that there are no repairs needed on a property (which is practically impossible). The second is that he has no vacancies (much more plausible, but still difficult).

So our final result for Jim is that after 20 years:
Houses: 2
Annual mortgage liability: $26,000
Annual income after mortgages/taxes/insurance: $35,000
Equity: $590,000

Now on to Pablo. Without having done the math here, I'd like to make the hypothesis that Pablo is going to be worth a tremendous amount more, but also be on the hook for an amazingly large amount of money each year. Remember that while Jim was pouring his returns into paying down existing mortgages, Pablo is going to be saving his returns until he can purchase a new rental property.

The math is going to be the same, except that we are going to have to include a new column for Pablo that holds his savings. I'll leave the calculations out of the article, since it's essentially the same as Jim, just more numerous. After year 7, Pablo has saved up $33,752, while houses in his area are worth $297,691. Therefore he now more than a 10% down payment and can go shopping for another house.


So we begin the dance with two homes, and again Pablo will be saving up for his third home. Predictably, this home take far less time to save for, and Pablo can now purchase his third home in only 4 more years. So in year 12, his account sheet might look something like this, right before he buys a third house:


This will keep compounding, so let's just cut to the big finish.

drum roll please.....

In year 20, Pablo's company looks like this:
Houses: 6
Annual mortgage liability: $132,102
Annual income after mortgages/taxes/insurance: $42,254
Equity: $902,459

By running some simple numbers we can conclude that Jim enjoyed an annualized return of 13.5% on his investment and Pablo earned a very impressive 16% return. And that was assuming a rather conservative annualized appreciation of 3% a year. And this was only on the original $47,000. Neither Jim nor Pablo put any of their own money into their business after the initial infusion.

So we can come to the final answer that after 20 years, Pablo's more reckless style of investing has pushing his annual return up by 2.5% (which is a very significant number) but at the cost of quintupling his risk (507% the annual liability of Jim). Obviously, most investors want to play it somewhere in the middle. The more leveraged you are (meaning a larger number of mortgages) the faster your money grows, but that money will have to be paid back whether or not you manage to collect rent.

I just want to make a few small notes to conclude:

• Neither Jim nor Pablo put any of the money aside in case of emergencies and or vacancies. This was very foolish of both of them. One possible modification to the model could be saving 10% of their annual rental income for emergencies. Which is the inspiration for the picture at the top of the post.
  
• Both Jim and Pablo will end up multi-millionaires by the time they retire IF they continue to save from their employment income and invest it either in other house or stocks (or hopefully both). They'd be fools not to continue to save aggressively.
  
• While Pablo's model pushes hard for equity growth, it's easy to see how Jim's model is great for cashflow. One possibility is melding the two models. Start by expanding aggressively (but not beyond your means) and then eventually switch over to Jim's system and pay off your mortgages one at a time. That could provide some serious income.
  
• Bear in mind that even if you disregard risk, Pablo is also managing 3 times as many houses as Jim. That's a lot of work and a lot of time. Jim's method might have been less lucrative, but it's also much more manageable by a busy investor. Keeping two houses occupied and their tenant's happy is by no means a full-time job, but it's gets harder with each unit you add to the mix.
  

The makings of a model

In this series we've been discussing how to use a little math and a lot of Excel to help you make better decisions in your investment activities. Landlord Schmandlord posts one of the landlord's great questions "Is it better to pay off each house, or buy when you have enough for a new down payment?" We've chosen to attempt to answer the question with two hypothetical people, Jim and Pablo.

Jim is our conservative investor. He plans on piping all of his excess cash flow into paying down his mortgage on his first rental property before purchasing a second. You can see a list of our complete set of assumptions here. Let's look at how we might go about calculating Jim's possible return...

Start by opening a new spreadsheet. Let's reserve the top two rows for the numbers our assumptions have gotten us. In fact, lets go ahead and put in our assumptions in the top two rows right now.

Let's go ahead and enter in the starting cost of our first home as well. We've decided to pay $235,000, and since we're giving Jim a 20% down payment, that means he's put $47,000 down on it. Now some of the math we'll do here (because it's fun) and some of the math we'll have done for us (to show that the answers you seek can often be found via the internet with a minimum of work done by you). The next step is to calculate our monthly payment. To do this we can simply go to any of a million mortgage calculators on the internet, through I prefer Bankrate.com. The monthly payment on our mortgage is $1206.89.

So now it time to do a little spreadsheet magic. So now that we have our assumptions, now we want to model his performance year after year. Let's start by figuring out his totals at the beginning of our test period. At the beginning (or Year 0), Jim owes $188,000 (the cost of the home - the down payment, or C4 - C5). He has $47,000 in equity.

His net income is equal to his gross income - his costs. We can calculate his gross income by multiplying his monthly rent by 12 (L1 * 12), for a total income of $18,000. His costs are his mortgage and his taxes and fees. His mortgage is a fixed amount so we can calculate that he will be paying $14,483 a year(D5), and his taxes are equal to .005 of the cost of his house (which we can calculate by adding his equity and his debt, or C7 + D7).

By putting that all together we figure out that the formula for his first year of income is equal to:
=(L1 * 12) - (D5 + .005 * (C7 + D7)) for an income of $2,342.

That's how much he's going to make after taxes, insurance and mortgage payments are made. To figure out his totals in Year 1 is going to take some slightly more complicated math. First let's start with his debt. The amount of Debt he owes at the end of year 1 is is equal to the debt he owed 1 year ago minus whatever principal he paid off. To calculate the amount of principal he paid off through his mortgage we're going to use a simple formula (which isn't perfect, but it's close enough). Last year he owed $188,000 and paid 6.65% interest on that (D7 * I2) for a total of $12,502. Therefore $1,981 was left over in his mortgage payments to pay off principal (D5 - (D7 * I2)). But we can't stop there. Jim is also going to be piping in the $2342 he earned from rent (F7).

So the formula we can use to determine the amount he owes at the end of his first year is:
=D7 - ((D5 - (D7 * I2)) + F7)

Now let's look at his equity. To figure out what our equity in the house is worth we follow a simple formula. Figure out what the house is worth, and then subtract what we owe. To figure out what the house is worth we use a slightly more complicated formula than we've been using so far:
(value of the house) = (starting value) * (1.0 + appreciation rate)^(number of years)

or in other words: =C4*((I1+1.0)^(B8)). To get to the equity in the house from there, we can simply subtract the Debt we have (D8).

Now we have to figure out what our rental income will be. While the mortgage payments have stayed the same, our rent and our taxes have increased slightly. We can calculate how much the rent has changed by using the same formula we used for the value of the home, but changing the starting value to starting rent, and the appreciation rate to the rent growth rate. To get the taxes value we use the same formula as before ( .005 * (equity + debt)).

That leaves us with a rental income formula of:
=((L1*12)*((L2 + 1)^(B8)) - ((C8+D8)*O1) - D5)

If you don't understand any of this go back and try again. The formulas look daunting, but if you take out a pen and paper and write out the word version of the formulas, then substitute the values, it should become clearer. So far we've been using math that anyone should be able to use (the only tricky part is explaining the formula to figure out the value of the home in a given year. Just take my word on that one.)

At this point we can extrapolate the formulas we've used for the end of year 1 for the end of year 2 (replacing year 0 numbers with year 1 numbers). We can quickly figure out the rental income, equity and debt of Jim in this model for any year...


We can see that by the end of year 15, Jim is making $11,730 a year in rental income and only owes another $1,174 on his rental home. It's getting late, and while the math and spreadsheet calculations I've been doing haven't been very trying, writing about them can be. So I'll leave off here with plenty of information to digest. Next time we'll see what happens in year 16 when Jim pays off his first mortgage and starts saving up for a down payment on a second rental home.

I'm finally married

I won't bore you with the details, but I finally said "I do" on Saturday the 16th. Both my new bride and I had a blast (though we're both still completely wiped out, but even so it's nice to get back to our more regular routines.

The post I had intended to write prior to the wedding was in response to a blog post I had read the week prior to that. Again by the infamous Casey (of '$2 million in debt by 24' fame), I was simply stunned by what I had read. As a real estate investor AND a new husband, let me give you some general advice about how to reconcile the two.

[...] right before the wedding, she found out that I was really “broke as a joke”. I even bought the ring on a credit card and went into debt for the marriage expenses. She came into the relationship with no debt and excellent credit expecting stability and married into a financial storm without really knowing it.

My sister got engaged and never really considered something like pre-marital counseling because to her it had religious connotations that she wasn't comfortable with. After she got married one of her friends was proposed to and told my sister that she and her fiance were attending some pre-martial counseling. Very curious, my sister asked "what exactly do they do at your counseling sessions?" Her friend told her that they were talking about sharing the workload at home (chores and such), going over finances, and opening up about all the things you don't typically talk about in polite company (your credit cards, salaries, and past). Stunned, my sister asked "Don't engaged people normally talk about that anyways?"

As Casey has pointed out to us, the answer is no. But there is really no excuse for that, as a married couple you should both be completely aware of each other's situation. Months before we had the ceremony, I sat my wife down, told her were all of my bank accounts were, gave her the addresses to all of the properties I have an ownership interest in and broke down the finances for each of them. She probably doesn't remember much in the way of specifics, but I showed here where I kept my books.

If I were struck by lightning on my wedding night and killed (which thankfully I wasn't), I'm confident that between my partner (Biff) and my wife, my estate would be properly taken care of. And that's really what it's about, making sure that her decision to get married is a fully informed one, and making certain that she'd be able to continue if I was incapacitated.

This has to be an even greater concern for solo investors. What if you were put into a coma for a month, would your spouse be able to keep your investments afloat during that time? Maybe he/she doesn't have the knack for investing/landlording and couldn't run your company for the next 10 years, but does your spouse know what houses you own, how many and where they are?

I told her not to worry about it. I have it under control.

These are words that I believe should never be uttered between husband and wife, except in trivial matters. I say that because the two are a partnership and whenever one has something to worry about, both have something to worry about. And even if you do take the lead in a situation, your spouse should be fully informed of that situation at all times. The notion of "Don't worry about it" harks back to a time when one spouse would dominate the other, and thus hold all the power and all the responsibility.

I’ve set some high expectations. No wonder she is feeling disappointed. I owe it to her to make it right.

What every husband owes his wife, and every wife owes her husband is to simply be themselves. The only expectation of you is to treat your spouse with honesty, respect and courtesy. After that, all burdens are shared equally by both of you. Any person who is disappointed in their marriage because the wealth isn't as great as they thought it would be is simply a fool to begin with.

And of course all of this comes around full circle. Being in real estate investing isn't like stocks, it's more like owning a small business. As such, it's easy to exaggerate wealth (and many people I know do) in order to impress people. But if the person you are trying to impress is your fiance, then maybe you're investing for the wrong reasons.

The good investors I've met don't invest to impress people and woo women, they do it for future security and, sometimes, for fun. And as good investors, they make sure that their investments are placed in a position to be well handled should ill tidings befall them. And as good spouses, they are equally concerned that their significant others should be able to handle their estates should the worst happen.

I'm extremely excited to start my new life with my new wife. She fully knows all of the risks I take by investing (especially in this choppy market) and she also knows all of the potential rewards. But win or lose, we'll go through it together and share the burdens or the riches equally. It's going to be a lot of fun.

P.S. Someone wrote a comment that said "If you want to get rich, don't marry". Actually he's wrong. The real rule is, "If you want to get rich, marry happily, don't get a divorce, and don't have kids". Married couples without children really collect the cash. Any potential taxation negatives are more then made up by lower averaged living expenses and financial accountability. But bear in mind that while finance should be a consideration when deciding on marriage and kids, they should obviously not be the only consideration.

Building a Model for Real Estate

In my last post I discussed the most crucial, most criticized and most remembered part of putting together a mathematical model: the assumptions. Today we are going to open up Excel (or some other spreadsheet program) and begin the fun work of making the model work.

But first I want to go back really quickly and respond to a comment made in my last post. While I supported most of my assumptions with historical evidence, I didn't provide links to one crucial assumption, the rate I expect house prices to appreciate. I claimed that historically housing prices were relatively close (within a percent or two) of inflation. The simplest evidence of home prices against inflation can be found in the US. Census Bureau:

Median US Home Price: Adjusted to 2000 Dollars

1940	1950	1960	1970	1980	1990	2000
$30,600	$44,600	$58,600	$65,300	$93,400	$101,100	$119,600

Extracting from that data you can determine that the annualized rate of return (adjusted for inflation) on a house bought in 1950 (and sold in 2000) is 1.99%, the annual return for a house bought in 1960 was 1.8%, for a house bought in 1970 is 2.04%. Most calculations regarding home data tends to omit the 1940's because of the effect World War 2 had on skewing housing statistics. So you can see that it's safe bet that housing since World War 2 has has a somewhat stable return over long periods of time of around 2%.

We're going to forget the original scenario of Jim and Pablo for a minute (which is quite complicated) and instead take a look at this scenario. When I quoted my number of 3% I hadn't really done any calculations to justify it, other than looking at a chart or two. But it's a great example of how we could use a model to figure out where housing currently is (according to historical trends) and what will happen to it over the next 20 years.

So all of the data that we extract came from 2000 or before (which makes sense because it came from the Census, who won't collect more data until 2010). So the current bubble isn't part of our records. Let's see where it fits, and how to do an extremely simple model of home prices. Since it's currently the year 2006, doing calculations using 2000 dollars doesn't make much sense, so first let's update our figures to 2006 dollars. The formula to do this is simple:

2006 value = 2000 value * (2001 inflation) * (2002 inflation) * (2003 inflation)....

We can grab the inflation numbers from the US Bureau of Labor Statistics (the inflation rate is the % change, located in the far right column). In other words, the median home price in 2000, adjusted for 2002 dollars is equal to:

$119,700 * 1.028 (inflation in 2001 was 2.8%) * 1.016 (the rate of inflation in 2002 was 1.6%) = $125,020

Extrapolating this up to 2006 dollars means that adjusted to today's dollars, the median home in 2000 was worth $135,700. If you are still trying to understand why we are adjusting for inflation, just remember that the value of a dollar changes over time. Changing from 2000 dollars to 2006 dollars may not seem significant, but a movie ticket that cost $0.25 in 1924 would cost $6.40 in 2006 (it must be a matinee). The bottom line is that your dollar isn't worth as much today as it was 5 years ago, so hopefully you have more dollars lying around.

Open up a spread sheet and choose a random square over to the right side of the sheet and insert a 1.02 there. That's our rate of return (adjusted for inflation). Then starting a column on the left side put our number of $135,700 (you can also put the year, 2000, to make it easier to keep track).

Right below the home value, we want to create a little formula that takes our 2000 value, and multiplies it by 1.02 (to account for our 2% appreciation, adjusted for inflation). If you do this right, you should see a value very close to $138,414 in that box. Then for 2002, we want to multiply our 2001 figure by 1.02 again. And so on, until we get to 2006.

In the above photo you can see in the fx box (at the top) the formula I have for square B4. What this tells us is that according to the model we just made, the median US home right now should be worth about $152,820. With the current median price of a US home at about $217,900, we can see that our model thinks that the US home market is currently over-priced by about 27%. (In other words, if the median home fell by 27% tomorrow, the market would be extremely close to our model.

Now it's time to point out the potential flaw in our model. The first was discussed at great length in our last post, the assumptions. Because this model is extremely simple, we only have one real assumption, that US home prices will appreciate at about 2% over inflation. If that's wrong, the entire basis of our model is off. Whether or not it's a reasonable assumption to make is left in your hands to decide.

So where is it going in the future? We can mock up a simple model for this as well. Let's assume that the average rate of inflation from 2000 to 2020 in 3% and that homes will average a 2% gain over that. Therefore homes will increase in value by 5% a year. We can go back to our spreadsheet, update the percent gain and then extrapolate the model to the year 2020:

In addition we can make ourselves the nice little chart that we saw up at the top of the post. So using our model we can predict the following:

Median US Home Price: Modelled

2000	2006	2010	2015	2020
$119,600	$160,275	$194,815	$248,639	$317,334

With the current median price of a US home at about $217,900, we can see that to reach a predicted value of about $317,600 in 2020, we'll be looking at growth of 2.77% each year (that's 2.77% flat out, not on top of inflation). That's actually pretty damn close to my original estimate of 3% a year.

Now about annualized returns, this doesn't mean that housing will go about by close to 2.77% this year and close to 2.77% next year and so on. The yearly fluctuations can be tremendous. Let's pretend that you hold a stock that you bought for $100. It gets some good press and gains 100% that year (ending at $200). The following year one of their products goes bad and they lose 25% (bringing it back to $150). Over the two year you held the stock, you gain 50%, which is an annual gain of about 22.5%. (note that it's not 25%. Due to the effects of compounding interest you can't just divide the total gain by the number of years you held it).

Housing is the same way as stocks. One year it may do well, the next it may not. We can get to our annualized gain of 2.77% over the next 14 years in many ways. Maybe it will climb 8% in 2007, maybe it will fall 30%. The model we constructed simply suggests that if you buy a house today and sell it in 2020 it will have appreciated by just less than 3% a year.

One final flaw to point out, this model uses national data which is nearly useless in real estate investing. Every local real estate market is different and every one could have it's own model made. While I would expect the US average to somewhat follow this model, it's practically impossible to invest in the US real estate average. If I think that stocks as a whole are going up by 20% in the next 2 years, I can invest on that theory by buying shares of an S&P 500
index fund. I cannot do the same with real estate.

That's both good and bad news. Some markets, like Phoenix, Washington DC and most of California are probably going to perform far worse than this model over the next14 years because they were pushing the national median up. Other places, such as most of the South and Midwest, could very likely outperform this model.

You could make a similar model yourself by looking up sale histories or appraisal histories in your town (both are public knowledge, and usually on the web at the county assessor's office) and determine if your market is currently above the predicted values or below.

So that's an extremely simple model. The next post I'm am probably going to talk about bit about marriage and money (since I am getting married a week from Saturday), and then I'll get back to dealing with our original question of who performs better, Jim or Pablo?

Ciao,
The Landlord

Doing the Math, How to Reinvest Your Gains

Landlord Schmandlord wrote a blog post on the 1st about whether it is better to pay off an existing mortgage with your profits, or reinvest in a new home. He makes some solid claims in there about getting higher returns and greater tax advantages by reinvesting your profits into a new property, and then ends his post with a call to "What do you guys think?" I've never been the short to back down from a challenge, so being a very techincal sort of person, I decided to go ahead and model his two scenarios and do the math to see which plan is better and by how much. And as I sat down and considered how I'd approach this, I realized that it's a great opportunity to share with you how I go about making models. Using only Excel and an internet connection, I'm going to walk you through how I go about trying to answer questions like these.

To be honest, I'm a bit of a geek and modelling is one of the more fun aspects of investing (at least for me). Questions like this are what I invest for. Afterall, it's extremely applicable (should I work on only one house at a time?) but the answer isn't immeaditely clear. For those of us that are less mathematically inclined, I'll try to give good layman explinations of everything I do, and what each figure means. My goal is for you to walk away after reading this and feel like you have a good understanding of how to approach a similar problem in the future (maybe when looking at buying a new investment property later on).

We're going to compare two scenarios, Jim and Pablo. Jim is going to buy a house and use all the profits from that house to pay off the mortgage. Once his mortgage is paid off, he'll save up for another down payment and do the same thing with a second house. Pablo, on the other hand, will save his profits from his first house until he has enough to make a down payment on a second. He'll then buy his second and save for his third. His mortgages will be paid strictly according to schedule. We'll project their networths 20 years from the start date and see who made it out on top.

The first thing we need to talk about are assumptions. There are many variables involved in real estate, things that we don't have a solid answer to until they actually happen (what will Jim's mortgage rate be? How much will it cost Pablo to fix a leaky roof? 10 years from now, what will rents be?). Since we can't claim to know the answers to these questions, we'll just build estimates into our model. Some of our assumptions will be as follows (with the important figures highlighted in red):

• Our mortgages will all be secured at 6.65%. According to Freddie Mac, the average mortgage secured last week was 6.14%. But we don't want to pay points (the average borrower paid 0.4) and a non-owner-occupied property usually gets a slightly higher rate.
• Our first house (for each) will be bought at $235,000. The median home price for Q3 in the US was $232,300.
• Our rents will start out at $1,500 per month. As I wrote in an earlier post about pricing, a common goal is to get rent to equal 1% of the value of the property, but that typically isn't possible with single family homes.
• The value of the homes will increase by an average of 3% a year over the next 20 years. Yes this is probably on the conservative side, but not by too much. Traditionally real estate appreciates at a pace just ahead of inflation, and we are coming down from one of the biggest bubbles of all-time.
• Rents will increase by 3% a year as well. For obvious reasons, rents go up when prices go up, and can come back down when prices come down.
• Annual taxes, insurance and association fees will equal 0.5% of the current value of the home (taxes will go up, even with a fixed rate mortgage).
• Jim and Pablo will only buy a house when they think it can produce a positive cashflow. Under our model that will mean a down payment of 10%.
• Jim and Pablo will each start out with 1 house, 20% down. The reason they start with 20% down is to help speed up the model and exaggerate the differences between the two, and do so while making very realistic starting conditions.
  

This is turning into a far longer article than I had originally anticipated, so I think I'll leave off here and pick it up again later.

But I'd like to take a second to talk about assumptions. Most everyone has heard that good old saying, "Assumptions make an ASS out of U and ME" (if you don't get it, just write the bolded letter down on a piece of paper).

Anyone who has every done mathematical proofs in college can attest to the fact that assumptions are everything. Many a mathematician has been told "your proof is untouchable... but I disgree with your assumptions." For example, I can mathematical prove the number of angel that can dance on the head of a pin, if I make an assumption about the size of an angel. The math I do may be perfect, but if the assumption is wrong all my work is for naught.

Maybe a more hard hitting example might be that infamous flipper Casey Serin. His business model (whether he realizes it or not) was validated in his head by the assumption that real estate prices would continue to climb. When that assumption failed, his entire "business" came crashing down around him, now he's on the hook for over $2 million. In fact you can take any business model and validate it or destroy it simply by changing the assumptions.

Assumptions are pretty scary stuff, they can destroy a business. So where are we supposed to get assumptions from? Well, like most "expert opinions", assumptions are simply guesses. Will real estate return an annualized 3% over the next 20 years? No one will know that until 2026.

So when choosing your assumptions, consider two things carefully.
What is the historical average? Housing has historically increased at a rate just over inflation. Unless you have some solid evidence that suggests that the historical trend will change, stay close to the trend.

Be pessimistic. In most things I want people to be optomistic. I'm a huge fan of the theory of self-fulfilling prophecies, that the act of believing something greatly increases it's chances of occuring. For example a student who honestly believes he's going to fail a class is always going to underperform an equal student who think he could do well (if you hadn't noticed the connection yet, the picture at the top is of Oedipus, a very famous self-fulfilling prophecy). But while I think that every entreprenuer needs to be hopelessly optomistic about their ventures, when making models I propose the opposite. Because if your model can withstand the worst conditions you forsee, then when things actually go well you'll be in fantastic shape.

Currently, in most of my models, I assume a annualized 3% appreciation from real estate over the next 15 years or so, which I believe is a fairly conservative estimate (depending on your area. Vegas and Phoenix might be lucky to average a annualized 3% return over 15 years). Over a shorter timeline, I'm much more pessimistic. Since the area I own in didn't over-inflate as much as the major cities, I tend to look at near 0% appreciation for the next 3-4 years (as a worst case scenario).

I'll continue this tomorrow when we go about setting up Excel to try to model Jim's busines


Updated: I just reached a major milestone. This was the first post I've written that contained no misspellings! Spellcheck just gave me the big thumb's up!

On Get Rich Quick Gurus....

I read a fabulous article the other day that I had to share. The title of the article is The Fallacy of Success and it was written in 1909. As you read it (or just the few passages I will comment on here) think of the dozens of late-night infomercials you've seen that will teach you to make millions in the next 1-5 years through No Money Down!

The author openly mocks "Success" authors, with a fictitious quote from a book about how to succeed at cards:

"In playing cards it is very necessary to avoid the mistake (commonly made by maudlin humanitarians and Free Traders) of permitting your opponent to win the game. You must have grit and snap and go in to win. The days of idealism and superstition are over. We live in a time of science and hard common sense, and it has now been definitely proved that in any game where two are playing IF ONE DOES NOT WIN THE OTHER WILL."

He follows that up with the quip, "It is all very stirring, of course; but I confess that if I were playing cards I would rather have some decent little book which told me the rules of the game." Then he continues on to recount an actual article he found in a popular magazine (probably akin to People today, or US Weekly). The article claims to describe the Instinct that Makes People Rich. It begins by recounting the story of Cornelius Vanderbilt, an American railroad tycoon and ends by telling us that "The precise opportunities that fell to him do not occur to us. [...] we can follow his general methods; we can seize those opportunities that are given us, and give ourselves a very fair chance of attaining riches". Of this extremely vague advice, Chesterton remarks:

In such strange utterances we see quite clearly what is really at the bottom of all these articles and books. It is not mere business; it is not even mere cynicism. It is mysticism; the horrible mysticism of money. The writer of that passage did not really have the remotest notion of how Vanderbilt made his money, or of how anybody else is to make his. He does, indeed, conclude his remarks by advocating some scheme; but it has nothing in the world to do with Vanderbilt. He merely wished to prostrate himself before the mystery of a millionaire.

When Chesterton wrote this in 1909 he obviously could not have known about Robert Allen, Carleton Sheets, Robert Kiyosaki or any of the other self-proclaimed "gurus" would start marketing their systems on late night cable. So the only possible conclusion is that marketers like these are nothing new. They are simply passing along the same advice that's been sold for over 100 years (and probably much longer.

An astute reader will note an uncommon similarity between the closing of the article ("we can seize those opportunities that are given us, and give ourselves a very fair chance of attaining riches") and the article I wrote on the lucky rich ("then watch for profitable opportunities and seize them"). Both make vague references to these mystic opportunities that occur which you can grab and wealth will be yours. However there's a difference between their madness and mine.

I will willingly admit that I have no idea what those opportunities are like. I'm vague about those opportunities because I lack the ability to describe them better. I know these opportunities exist because of how others (like Bill Gates or Steve Jobs) have seized them, but that hardly makes me an expert.

The entire purpose of my previous article was to dissuade readers from relying on the dream of the lucky rich to fuel their future. While I don't know about how to create hundreds of millions of dollars in wealth in the next 10 years, I do know how to create $1 million in wealth over the next 20 (currently on track to break my first million in my mid 30's, without any windfalls or inheritances).

Are you aiming to join the wealthy elite with net-worths over $50 million? Best of luck, I know it's possible to get there and I'll cheer you on all the way, but don't ask me for guidance. The best I can do is help you try to build that $2-$5 million safety net... You know... Just in case that huge deal doesn't go through...