The makings of a model

In this series we've been discussing how to use a little math and a lot of Excel to help you make better decisions in your investment activities. Landlord Schmandlord posts one of the landlord's great questions "Is it better to pay off each house, or buy when you have enough for a new down payment?" We've chosen to attempt to answer the question with two hypothetical people, Jim and Pablo.

Jim is our conservative investor. He plans on piping all of his excess cash flow into paying down his mortgage on his first rental property before purchasing a second. You can see a list of our complete set of assumptions here. Let's look at how we might go about calculating Jim's possible return...

Start by opening a new spreadsheet. Let's reserve the top two rows for the numbers our assumptions have gotten us. In fact, lets go ahead and put in our assumptions in the top two rows right now.

Let's go ahead and enter in the starting cost of our first home as well. We've decided to pay $235,000, and since we're giving Jim a 20% down payment, that means he's put $47,000 down on it. Now some of the math we'll do here (because it's fun) and some of the math we'll have done for us (to show that the answers you seek can often be found via the internet with a minimum of work done by you). The next step is to calculate our monthly payment. To do this we can simply go to any of a million mortgage calculators on the internet, through I prefer Bankrate.com. The monthly payment on our mortgage is $1206.89.

So now it time to do a little spreadsheet magic. So now that we have our assumptions, now we want to model his performance year after year. Let's start by figuring out his totals at the beginning of our test period. At the beginning (or Year 0), Jim owes $188,000 (the cost of the home - the down payment, or C4 - C5). He has $47,000 in equity.

His net income is equal to his gross income - his costs. We can calculate his gross income by multiplying his monthly rent by 12 (L1 * 12), for a total income of $18,000. His costs are his mortgage and his taxes and fees. His mortgage is a fixed amount so we can calculate that he will be paying $14,483 a year(D5), and his taxes are equal to .005 of the cost of his house (which we can calculate by adding his equity and his debt, or C7 + D7).

By putting that all together we figure out that the formula for his first year of income is equal to:
=(L1 * 12) - (D5 + .005 * (C7 + D7)) for an income of $2,342.

That's how much he's going to make after taxes, insurance and mortgage payments are made. To figure out his totals in Year 1 is going to take some slightly more complicated math. First let's start with his debt. The amount of Debt he owes at the end of year 1 is is equal to the debt he owed 1 year ago minus whatever principal he paid off. To calculate the amount of principal he paid off through his mortgage we're going to use a simple formula (which isn't perfect, but it's close enough). Last year he owed $188,000 and paid 6.65% interest on that (D7 * I2) for a total of $12,502. Therefore $1,981 was left over in his mortgage payments to pay off principal (D5 - (D7 * I2)). But we can't stop there. Jim is also going to be piping in the $2342 he earned from rent (F7).

So the formula we can use to determine the amount he owes at the end of his first year is:
=D7 - ((D5 - (D7 * I2)) + F7)

Now let's look at his equity. To figure out what our equity in the house is worth we follow a simple formula. Figure out what the house is worth, and then subtract what we owe. To figure out what the house is worth we use a slightly more complicated formula than we've been using so far:
(value of the house) = (starting value) * (1.0 + appreciation rate)^(number of years)

or in other words: =C4*((I1+1.0)^(B8)). To get to the equity in the house from there, we can simply subtract the Debt we have (D8).

Now we have to figure out what our rental income will be. While the mortgage payments have stayed the same, our rent and our taxes have increased slightly. We can calculate how much the rent has changed by using the same formula we used for the value of the home, but changing the starting value to starting rent, and the appreciation rate to the rent growth rate. To get the taxes value we use the same formula as before ( .005 * (equity + debt)).

That leaves us with a rental income formula of:
=((L1*12)*((L2 + 1)^(B8)) - ((C8+D8)*O1) - D5)

If you don't understand any of this go back and try again. The formulas look daunting, but if you take out a pen and paper and write out the word version of the formulas, then substitute the values, it should become clearer. So far we've been using math that anyone should be able to use (the only tricky part is explaining the formula to figure out the value of the home in a given year. Just take my word on that one.)

At this point we can extrapolate the formulas we've used for the end of year 1 for the end of year 2 (replacing year 0 numbers with year 1 numbers). We can quickly figure out the rental income, equity and debt of Jim in this model for any year...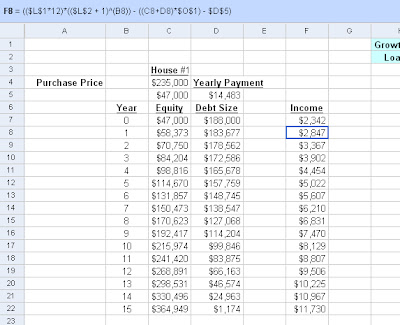


We can see that by the end of year 15, Jim is making $11,730 a year in rental income and only owes another $1,174 on his rental home. It's getting late, and while the math and spreadsheet calculations I've been doing haven't been very trying, writing about them can be. So I'll leave off here with plenty of information to digest. Next time we'll see what happens in year 16 when Jim pays off his first mortgage and starts saving up for a down payment on a second rental home.